HashMap源码解析

发表于 | 分类于 | 评论数： | 阅读次数：
本文字数： 26k | 阅读时长 ≈ 24 分钟

以后面试官问你HashMap原理，不能再答数组+链表的结构了，JDK1.8 添加了红黑树结构，知识要与时俱进啊。受限于文章篇幅，我会从HashMap 初始化，put、get、remove方面解析底层原理。

内部设定

常量设定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * HashMap 默认初始化长度
 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

/**
 * HashMap 允许容器数组最大长度
 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/**
 * 负载因子，容器数量/容器最大长度 大于等于，数组进行扩容
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 *  链表的长度超过阈值，在添加元素的时候链表转化成红黑树
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * 在扩容的时候，红黑树数量小于阈值转换成链表
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * table数组支持红黑树链最少数组长度
 */
static final int MIN_TREEIFY_CAPACITY = 64;

内部元素结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
static class Node<K,V> implements Map.Entry<K,V> {
       final int hash;
       final K key;
       V value;
       Node<K,V> next;

       Node(int hash, K key, V value, Node<K,V> next) {
           this.hash = hash;
           this.key = key;
           this.value = value;
           this.next = next;
       }

       public final K getKey()        { return key; }
       public final V getValue()      { return value; }
       public final String toString() { return key + "=" + value; }

       public final int hashCode() {
           return Objects.hashCode(key) ^ Objects.hashCode(value);
       }

       public final V setValue(V newValue) {
           V oldValue = value;
           value = newValue;
           return oldValue;
       }

       public final boolean equals(Object o) {
           if (o == this)
               return true;
           if (o instanceof Map.Entry) {
               Map.Entry<?,?> e = (Map.Entry<?,?>)o;
               if (Objects.equals(key, e.getKey()) &&
                   Objects.equals(value, e.getValue()))
                   return true;
           }
           return false;
       }
   }

Node对象只拥有三个属性，key，value，next，结构非常简单，操作也简单。

内部属性变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
  * 内部数组，上面所说table 指的就是这个
  */
 transient Node<K,V>[] table;

 /**
  * entrySet() 返回容器
  */
 transient Set<Map.Entry<K,V>> entrySet;

 /**
  * 键值对的数量，也是HashMap size
  */
 transient int size;

 /**
  * HashMap 结构修改次数
  */
 transient int modCount;

 /**
  * 扩容table 阈值
  */
 int threshold;

 /**
  *  扩容因子
  */
 final float loadFactor;

解析代码

构造函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }
    /**
     * Constructs an empty <tt>HashMap</tt> with the specified initial
     * capacity and the default load factor (0.75).
     *
     */
    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }

    /**
     * Constructs an empty <tt>HashMap</tt> with the default initial capacity
     * (16) and the default load factor (0.75).
     */
    public HashMap() {
        this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
    }

这段代码很简单，主要是判断两个输入参数是否合法，将容器长度重新计算扩容阈值。
看下tableSizeFor怎么计算阈值

1
2
3
4
5
6
7
8
9
10
11
12
/**
     * Returns a power of two size for the given target capacity.
     */
    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

这个方法其实通过输入数，返回一个最接近大于等于他的2次方数。
通过将cap 高位1不断右移，返回cap最近2次方的数。如果有同学看不懂这个算法，可以参考这位老哥写的https://blog.csdn.net/fan2012huan/article/details/51097331，解析得非常易懂。
上面的构造函数，并没有初始化Node 数组，我进入put方法看下怎么样初始化的！

添加元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

/**
 * @param hash hash for key
 * @param key the key
 * @param value the value to put
 * @param onlyIfAbsent if true, don't change existing value
 * @param evict if false, the table is in creation mode.
 * @return previous value, or null if none
 */
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
   //p 如果存在就是链头
    Node<K,V>[] tab; Node<K,V> p; int n, i;
     //数组未初始化
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
     //根据hash 值 计算数组下标位置，这个位置下没有元素
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null); //插入元素
    else {//hash 值冲突
        Node<K,V> e; K k;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k)))) //key 相等
            e = p;
        else if (p instanceof TreeNode) //红黑树
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else { 
            for (int binCount = 0; ; ++binCount) { //遍历链表，插入数据
                if ((e = p.next) == null) { //下一个元素为空，说明已经遍历到最后一个元素 ，插入 终止循环
                    p.next = newNode(hash, key, value, null);
                    if (binCount >= TREEIFY_THRESHOLD - 1) // 到达转化成树链的阈值
                        treeifyBin(tab, hash); //将链表转换成树
                    break;
                }
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k)))) //出现key 相等
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e); //空方法 ，LinkedHashMap 实现
            return oldValue;
        }
    }
    ++modCount;
    if (++size > threshold) //超出阈值 
        resize();
    afterNodeInsertion(evict);
    return null;
}

整体流程： 先判断数组为空，没有则使用resize()方法初始化数组，使用hash 值& 数组长度计算下标，下标值为空，直接插入。处理hash冲突情况，先判断链头key是否相等，判断数组Node是否树链，则使用putTreeVal方法插入树链中，否则遍历链表在结尾插入。最后判断数组元素是否超过阈值，使用reszie()扩容。这个流程基本和我们平常写业务代码差不多。

计算hash方法

1
2
3
4
static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }

假设没有这个hash算法，对象hashCode直接&数组长度(n-1),当n比较小的时候，hash虽然是32位整数，但是只要低位是有效的，hash冲突概率比较大，会导致链表比较长。使用hash方法将高16位影响到低16位，将低16位的二进制打散了，减少了hash冲突概率。
resize扩容，初始化数组方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        if (oldCap >= MAXIMUM_CAPACITY) { //大于最大数组长度，不会进行扩容操作
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // 使用构造函数cap初始化数组长度
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; //创建新数组
    table = newTab;
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null; //删除数组元素
                if (e.next == null)  //没有链表的元素，直接移动插入
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode)
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); //切割树链
                else { //将链条分成两个链条，一个是原数组下标，另一个则下标 x 2移动下标
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null); //将两种链条的链头元素插入到数组中
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

整体流程还是比较简单的，先确定数组长度，threshold属性，创建新数组移动copy元素，删除原数组元素。这个方法基本就是初始化table数组，扩容数组，处理链条或树链的内部细节。
if ((e.hash & oldCap) == 0) { 这个写法，看了好久才明白什么意思啊。我们都知道数组长度永远都是2的次方，二进制表现就是最高位是1 其他都是0， 比如默认长度16 ，二进制就是10000。 计算数组长度算法e.hash & (oldCap- 1)， 长度-1 二机制的数1111,先数组扩容长度 * 2，计算下标结果下标前面不变，最高位是0还是1，是0保存下标不变，是1表示下标需要x 2.。觉得讲得不清楚，可以看下图
image
下面了解拆分树链的split

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**     
         * @param map the map
         * @param tab the table for recording bin heads
         * @param index the index of the table being split
         * @param bit the bit of hash to split on
         */
        final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
            TreeNode<K,V> b = this;
            // 按hash 计算结果区分两个树链，统计树链的长度
            TreeNode<K,V> loHead = null, loTail = null;
            TreeNode<K,V> hiHead = null, hiTail = null;
            int lc = 0, hc = 0;
            for (TreeNode<K,V> e = b, next; e != null; e = next) {
                next = (TreeNode<K,V>)e.next;
                e.next = null;
                if ((e.hash & bit) == 0) {
                    if ((e.prev = loTail) == null)
                        loHead = e;
                    else
                        loTail.next = e;
                    loTail = e;
                    ++lc;
                }
                else {
                    if ((e.prev = hiTail) == null)
                        hiHead = e;
                    else
                        hiTail.next = e;
                    hiTail = e;
                    ++hc;
                }
            }

            if (loHead != null) {
                if (lc <= UNTREEIFY_THRESHOLD)
                    tab[index] = loHead.untreeify(map); //拆分树链转化成链条结构
                else {
                    tab[index] = loHead;
                    if (hiHead != null) // (else is already treeified)
                        loHead.treeify(tab);
                }
            }
            if (hiHead != null) {
                if (hc <= UNTREEIFY_THRESHOLD)
                    tab[index + bit] = hiHead.untreeify(map);
                else {
                    tab[index + bit] = hiHead;
                    if (loHead != null)
                        hiHead.treeify(tab);
                }
            }
        }

首先要知道TreeNode间接继承Node，拥有单向链条的属性。理解上面流程就很简单了，先遍历树链，按照hash & 数组长度方式，分成移动下标和不移动两个类型树链。再判断链条数量是否大于UNTREEIFY_THRESHOLD(6) ,满足使用untreeify方法拆分成链条。如果树链头不为空，则说明红黑树结构依然存在，使用treeify方法将链表转换成树链。
要理解链表怎么转化成树链，必须深入treeify方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
final void treeify(Node<K,V>[] tab) {
    TreeNode<K,V> root = null;
    //从this 链头开始遍历
    for (TreeNode<K,V> x = this, next; x != null; x = next) {
        next = (TreeNode<K,V>)x.next;
        x.left = x.right = null;
        if (root == null) { //root 根元素
            x.parent = null;
            x.red = false;
            root = x;
        }
        else {
            K k = x.key;
            int h = x.hash;
            Class<?> kc = null;
            for (TreeNode<K,V> p = root;;) {
                int dir, ph;
                K pk = p.key;
                if ((ph = p.hash) > h)
                    dir = -1;
                else if (ph < h)
                    dir = 1;
                else if ((kc == null &&
                          (kc = comparableClassFor(k)) == null) ||
                         (dir = compareComparables(kc, k, pk)) == 0)
                    dir = tieBreakOrder(k, pk);

                TreeNode<K,V> xp = p;
                if ((p = (dir <= 0) ? p.left : p.right) == null) { //如果子节点黑红都是null，直接插入指向，否则向下递归
                    x.parent = xp;
                    if (dir <= 0)
                        xp.left = x;
                    else
                        xp.right = x;
                    root = balanceInsertion(root, x); //调整节点位置，着色，左旋或者右旋
                    break;
                }
            }
        }
    }
    moveRootToFront(tab, root); //判断root是否根节点，如果不是插入根节点位置
}

看到这里，大家是不是跟我一样，觉得代码写得还是比较简单的，没什么难度啊。下面代码就不是这样了，没有一点黑红树基础的同学，麻烦先补下课先，不然你很难理解代码什么意思。

红黑树的性质
  1. 节点是红色或黑色。
  2. 根节点是黑色。
  3. 所有叶子都是黑色（叶子是NIL节点）
  4. 每个红色节点的两个孩子节点必须是黑色. (从叶子到根的所有路径上不能有两个连续的红色节点)
  5. 从任意节点到其叶子节点的所有路径都包含相同数目的黑色节点。

红黑树.png
在红黑树插入或删除情况，上面的特征可能会被打破。所以要使用balanceInsertion方法平衡树链结构。我们在分析代码的时候，一定要把上面5个性质带上有助于理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
                                                    TreeNode<K,V> x) {
            x.red = true; //默认x 就是红色 
            for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
                //x 的父节点xp为空，则说明x 就是根节点 , 根据1属性，节点变成黑色就可以了
                if ((xp = x.parent) == null) {
                    x.red = false;
                    return x;
                }
                //父节点黑色，插入红色，以上条件都满足，终止循环
                else if (!xp.red || (xpp = xp.parent) == null)
                    return root;
               
                if (xp == (xppl = xpp.left)) {
                    //见图1-1 ，不满足性质4、性质5，改变着色，向上递归
                    if ((xppr = xpp.right) != null && xppr.red) {
                        xppr.red = false;
                        xp.red = false;
                        xpp.red = true;
                        x = xpp;
                    }
                    else {
                        //见图1-2 不满足 性质4，xp左移 
                        if (x == xp.right) {
                            root = rotateLeft(root, x = xp);
                            xpp = (xp = x.parent) == null ? null : xp.parent;
                        }
                        // 图1-3情况 不满足性质4，xpp 右移 调整着色
                        if (xp != null) {
                            xp.red = false;
                            if (xpp != null) {
                                xpp.red = true;
                                root = rotateRight(root, xpp);
                            }
                        }
                    }
                }
                else { //位置相反，流程一样，位置互换即可
                    if (xppl != null && xppl.red) {
                        xppl.red = false;
                        xp.red = false;
                        xpp.red = true;
                        x = xpp;
                    }
                    else {
                        if (x == xp.left) {
                            root = rotateRight(root, x = xp);
                            xpp = (xp = x.parent) == null ? null : xp.parent;
                        }
                        if (xp != null) {
                            xp.red = false;
                            if (xpp != null) {
                                xpp.red = true;
                                root = rotateLeft(root, xpp);
                            }
                        }
                    }
                }
            }
        }

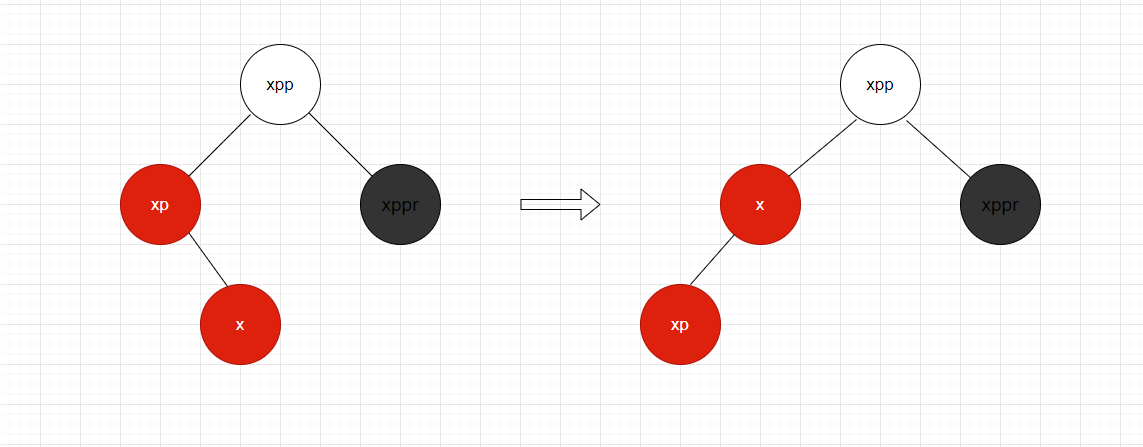
上面的代码配合这三个图片，看出1-3 处理完后，刚好是图1-1 处理条件，向上递归，直到终止循环。这个就是插入后，调整红黑树平衡整体流程。这些代码，我当时看了一整天也明白什么意思，后面结合红黑树知识，自己画图对应代码流程，理解起来就很简单了。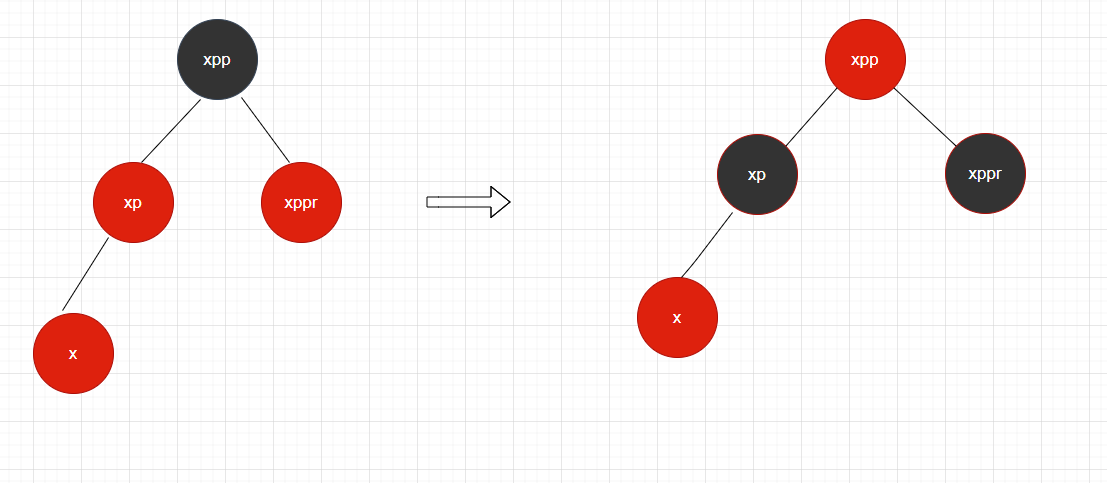
图1-1
图1-2
图1-3
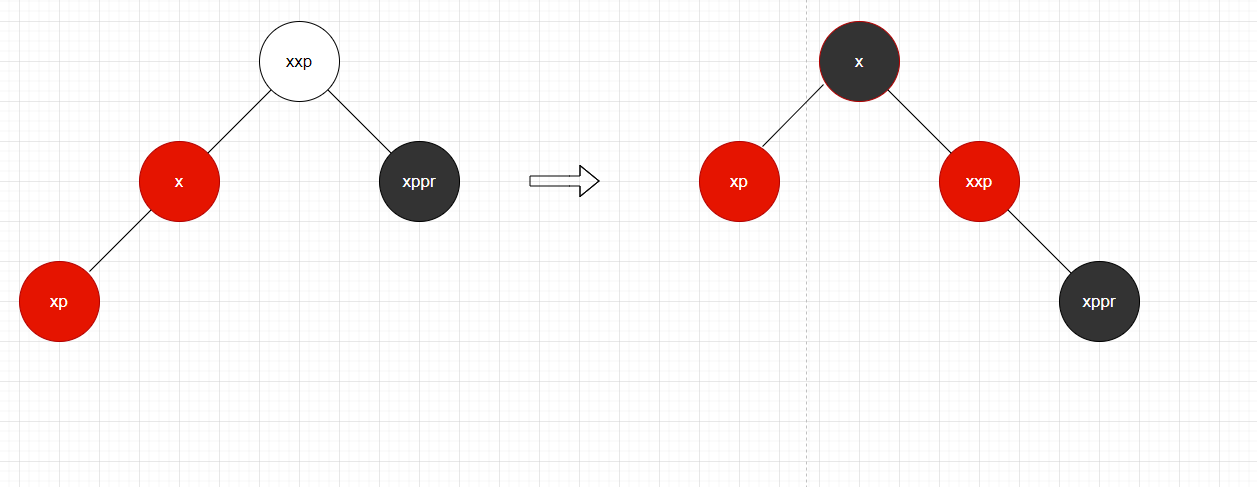
有了这些理解在去看putTreeVal方法就很简单了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Tree version of putVal.
 */
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                               int h, K k, V v) {
    Class<?> kc = null;
    boolean searched = false;
    TreeNode<K,V> root = (parent != null) ? root() : this;
    for (TreeNode<K,V> p = root;;) {
        int dir, ph; K pk;
        if ((ph = p.hash) > h)
            dir = -1;
        else if (ph < h)
            dir = 1;
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p;
       // 获取key 类型，判断是是compare接口 比较大小
        else if ((kc == null &&
                  (kc = comparableClassFor(k)) == null) ||
                 (dir = compareComparables(kc, k, pk)) == 0) {
            if (!searched) {
                TreeNode<K,V> q, ch;
                searched = true;
                if (((ch = p.left) != null &&
                     (q = ch.find(h, k, kc)) != null) ||
                    ((ch = p.right) != null &&
                     (q = ch.find(h, k, kc)) != null))
                    return q;
            }
            dir = tieBreakOrder(k, pk); //使用类名，原生hash比较大小
        }

        TreeNode<K,V> xp = p;
        if ((p = (dir <= 0) ? p.left : p.right) == null) {
            Node<K,V> xpn = xp.next;
            TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
            if (dir <= 0)
                xp.left = x;
            else
                xp.right = x;
            xp.next = x;
            x.parent = x.prev = xp;
            if (xpn != null)
                ((TreeNode<K,V>)xpn).prev = x;
            moveRootToFront(tab, balanceInsertion(root, x));
            return null;
        }
    }
}

遍历树链，比较hash 大小，找到子节点插入位置，使用balanceInsertion方法平衡红黑树。

获取value get()方法分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    if ((tab = table) != null && (n = tab.length) > 0 && //空数组不指望了
        (first = tab[(n - 1) & hash]) != null) { //计算数组下标位置
        if (first.hash == hash && // 获取到value 
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        if ((e = first.next) != null) {
            if (first instanceof TreeNode) //使用红黑树查找
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null); //先查找，在遍历
        }
    }
    return null;
}

看下红黑树查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
final TreeNode<K,V> getTreeNode(int h, Object k) {
    return ((parent != null) ? root() : this).find(h, k, null);
}

final TreeNode<K,V> root() {
    for (TreeNode<K,V> r = this, p;;) {
        if ((p = r.parent) == null)
            return r;
        r = p;
    }
}

final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
    TreeNode<K,V> p = this;
    do {
        int ph, dir; K pk;
        TreeNode<K,V> pl = p.left, pr = p.right, q;
        if ((ph = p.hash) > h) //大于往左边
            p = pl;
        else if (ph < h) //小于往右边
            p = pr;
        else if ((pk = p.key) == k || (k != null && k.equals(pk))) //找到了
            return p;
        else if (pl == null) //遍历到最底下一个节点为止，这个p节点肯定没有字节点
            p = pr;
        else if (pr == null)
            p = pl;
        else if ((kc != null ||
                  (kc = comparableClassFor(k)) != null) &&
                 (dir = compareComparables(kc, k, pk)) != 0)
            p = (dir < 0) ? pl : pr;
        else if ((q = pr.find(h, k, kc)) != null)
            return q;
        else
            p = pl;
    } while (p != null);
    return null;
}

删除节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public V remove(Object key) {
    Node<K,V> e;
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
        null : e.value;
}
final Node<K,V> removeNode(int hash, Object key, Object value,
                           boolean matchValue, boolean movable) {
    Node<K,V>[] tab; Node<K,V> p; int n, index;
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (p = tab[index = (n - 1) & hash]) != null) {
        Node<K,V> node = null, e; K k; V v;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))  //根据key 找到value
            node = p;
        else if ((e = p.next) != null) {
            if (p instanceof TreeNode)
                node = ((TreeNode<K,V>)p).getTreeNode(hash, key); //使用红黑树寻找
            else {
                do { //链表遍历查找
                    if (e.hash == hash &&
                        ((k = e.key) == key ||
                         (key != null && key.equals(k)))) { 
                        node = e;
                        break;
                    }
                    p = e;
                } while ((e = e.next) != null); 
            }
        }
        if (node != null && (!matchValue || (v = node.value) == value ||
                             (value != null && value.equals(v)))) {
            if (node instanceof TreeNode)
                ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable); //在红黑树中删除，这个有点复杂
            else if (node == p) //如果p刚好是链头，指引删除
                tab[index] = node.next;
            else //p 刚好表示前一位，node 要被删除，p指向node 下一个节点，即可删除。
                p.next = node.next;
            ++modCount;
            --size;
            afterNodeRemoval(node);
            return node;
        }
    }
    return null;
}

数组和链表删除还是比较简单的，下标指引变更即可。红黑树元素删除就相当复杂了，比插入数据要麻烦等多了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
                          boolean movable) {
    int n;
    if (tab == null || (n = tab.length) == 0)
        return;
    int index = (n - 1) & hash;
    TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
    TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
    if (pred == null) //前置节点为空，将链头指向succ，即子节点
        tab[index] = first = succ;
    else  //将前置节点指向next，相当于删除this
        pred.next = succ;
    if (succ != null) //删除
        succ.prev = pred;
    if (first == null)
        return;
    if (root.parent != null)
        root = root.root();
    if (root == null //根据红黑树特性，最短路径不能小于最长路径1/2，树链长度不足 2 +4 = 6，拆分
        || (movable
            && (root.right == null
                || (rl = root.left) == null
                || rl.left == null))) {
        tab[index] = first.untreeify(map);  // too small
        return;
    }
    TreeNode<K,V> p = this, pl = left, pr = right, replacement;
    if (pl != null && pr != null) {
        TreeNode<K,V> s = pr, sl;
        while ((sl = s.left) != null) // 找到右孩子的左子树找最小值
            s = sl;
        boolean c = s.red; s.red = p.red; p.red = c; // 交换颜色
        TreeNode<K,V> sr = s.right;
        TreeNode<K,V> pp = p.parent;
        if (s == pr) { // s 是  p直系右子节点 ，交换位置
            p.parent = s;
            s.right = p;
        }
        else {
            TreeNode<K,V> sp = s.parent;
            if ((p.parent = sp) != null) { //p 移动到s 位置
                if (s == sp.left)
                    sp.left = p;
                else
                    sp.right = p;
            }
            if ((s.right = pr) != null) //s 移动到位置
                pr.parent = s;
        }
        p.left = null;
        if ((p.right = sr) != null)   //p 右节点 和s 关联
            sr.parent = p;
        if ((s.left = pl) != null)  //s 和p子左边节点pl关联起来
            pl.parent = s;
        if ((s.parent = pp) == null) // s 父节点 指向 p 父节点  s 已经完全替换p 
            root = s;
        else if (p == pp.left) 
            pp.left = s;
        else
            pp.right = s;
        if (sr != null)
            replacement = sr;
        else
            replacement = p;
    }
    else if (pl != null) //只有左节点情况
        replacement = pl;
    else if (pr != null) //只有右节点情况
        replacement = pr;
    else
        replacement = p;
    if (replacement != p) {
        TreeNode<K,V> pp = replacement.parent = p.parent;
        if (pp == null)
            (root = replacement).red = false;
        else if (p == pp.left)
            pp.left = replacement;
        else
            pp.right = replacement;
        p.left = p.right = p.parent = null;
    }
    //调整元素在红黑树中着色，保持平衡
    TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);

    if (replacement == p) {  // 删除元素p
        TreeNode<K,V> pp = p.parent;
        p.parent = null;
        if (pp != null) {
            if (p == pp.left)
                pp.left = null;
            else if (p == pp.right)
                pp.right = null;
        }
    }
    if (movable)
        moveRootToFront(tab, r);
}

简单说一下，这个方法代码是思路，首先处理最简单的链表删除元素，将链表中对象的引用改成旁边的元素。
红黑树删除元素则比较复杂点，考虑的情况比较多。比如删除节点在底下，没有子节点，就可以直接删除，最为简单了，红黑树的删除就是将复杂节点位置，变成简单的方式处理。这个方法大部分代码都是在处理左右节点不为空的情况，将删除节点位置和右节点下最左边的子节点交换位置，并且交换着色。为什么要这么做呢？主要是因为这个节点的hash值和删除节点值最为接近，红黑树的特性小于在左边，大于在右边，大于删除值的最小值，就整个红黑树最接近删除的值。在调整红黑树着色，任务就算完成了。

心得

整体来说HashMap的代码并不是很复杂，底层业务代码，其实就跟我们平常写的crud代码。但是我在看代码的时候，有一些地方好难看懂啊，主要是涉及到红黑树的知识点。很多程序员（包括我）平常都会抱怨数据结构没什么用，在工作中用不上，其实我们掌握不够熟练，在工作上不知道使用。

参考文献

红黑树特性
hash算法解析